PÓKERVILÁG

II. Valószínűségszámítási alapismeretek

II.1. A véletlen esemény

A véletlen felfogása alapvetően kétféle lehet. Az ún. determinisztikus világképben a véletlen egyszerűen a tudásunk hiányát jelenti. Mivel nem tudunk minden adatot, ezért nem tudjuk meghatározni, mi fog történni, de ha ismernénk minden információt, akkor a véletlen megszűnne. A másik felfogás szerint a véletlen alapvető része a világnak, ezért akkor sem tudnánk megmondani, hogy mi történik, ha ismernénk minden adatot egy adott problémával kapcsolatban.

Hasonló a helyzet a valószínűséggel. Nem tudjuk pontosan eldönteni, hogy egy adott helyzetben, pl. kockával dobva a dobott értékek bekövetkezésének valószínűsége csak a kockától függ-e, tehát ún. objektív valószínűsége van-e, vagy pedig valami más tényező is befolyásolja ezt. Sokszor ebben a problémában az „elegendő ok hiánya” dönt: nincs okunk azt feltételezni, hogy egy adott kísérlet kimenetelei nem szimmetrikusak, tehát objektív valószínűséget tételezünk fel. Persze más kérdés az, hogy az objektív valószínűségről hogy lehet eldönteni, hogy mekkora az értéke?

Próbálkozhatunk modellalkotással is. Laplace (1812) az ún. klasszikus modellt alkalmazta: egy esemény bekövetkezésének valószínűsége a kedvező esetek száma osztva az összes esetek számával. Eszerint az úgynevezett elemi események (ami az „összes esetekből” egy darabot jelent) valószínűsége meg kell egyezzen. De milyen jogon mondhatjuk, hogy az egyes elemi események valószínűsége megegyezik? Ugyanoda jutottunk vissza, ahonnan elindultunk.

Kolgomorov (1933) tovább lépett. Azt mondta: axiómákat, tehát nem bizonyítandó (és nem is bizonyítható) állításokat kell felállítani a valószínűségről, és ezek segítségével fel kell építeni a valószínűség-fogalmat. [Tömören: Metrikának nevezzük azt a hozzárendelést, amelyben egy alaphalmaz részhalmazaihoz számértékeket rendelünk. A hozzárendelt értékeket az adott részhalmaz mértékszámának nevezzük. Egy metrika akkor valószínűség, ha az alaphalmazhoz rendelt értéke 1, nem negatív és additív (diszjunkt részhalmazok mértékének összege az uniójukhoz rendelt mérték).] Ezzel azonban szintén nem jutottunk közelebb ahhoz a problémához, hogy a kockával mekkora valószínűséggel dobunk hatost.

Szeretnénk tehát egy olyan állapotot elérni, amiben az a helyzet áll fenn, hogy bár nem tudunk mindent (ez tény), de a nemtudásunknak ne legyen nagy kockázata.

Kezdjük tehát előlről, építsünk fel egy modellt, aztán próbáljuk meg megvizsgálni, hogy ez a modell mennyire jó.

II.2. Klasszikus valószínűségszámítási modell

A valószínűségszámításban használni fogunk néhány fogalmat, ismerkedjünk meg ezekkel! Kísérletnek nevezünk valamely folyamatot, melyben a véletlen dönti el, hogy mi fog történni. A kísérletek általában megismételhetőek (mi itt ilyen kísérletekkel foglalkozunk), de kimenetelük nem feltétlenül lesz ugyanaz, mint egy korábbi kísérletben. Egy kísérlet lehetséges kimeneteleiből képezhetünk halmazokat; ezeket nevezzük eseményeknek. Például dobókockával egyszer dobva a kockadobás lehetséges kimenetelei 1, 2, 3, 4, 5, 6; esemény például, hogy páros számot dobtunk, vagy hogy 3-mal osztható számot dobtunk, de az is esemény, hogy pozitív számot dobtunk. Lehetetlen eseménynek nevezzük azokat az eseményeket, melyekhez nem tartozik egyetlen kimenet sem (pl. dobókockával nem egész számot dobunk), biztos eseménynek nevezzük azokat az eseményeket, melyekhez az összes lehetséges kimenetel hozzátartozik (pl. dobókockával dobva egész számot dobunk).

A leíró statisztikában szerepeltek az alábbi fogalmak: relatív gyakoriság, módusz, átlag, medián, szórás. Próbáljunk meg ezeknek valamiféle megfelelőt találni.

A relatív gyakoriság azt jelenti, hogy egy adott adathalmazban egy adat hányszor fordul elő. Ha a valószínűségről az a képünk van, hogy adott számú kísérletből az esemény bekövetkezéseinek száma arányos a bekövetkezésének valószínűségével, akkor a valószínűségre a relatív gyakoriságnak megfelelő értéket kell adnunk. Tekintsünk egy adott kísérletsorozatot, amely annyi kísérletből áll, ahány lehetséges kimenetele van a kísérleteknek. Tételezzük fel, hogy minden lehetséges kimenetel pontosan egyszer következik be a kísérletsorozatban (ez persze meglehetősen hihetetlennek tűnik). Egy adott esemény pontosan annyiszor következett be, ahányféle lehetséges kimenetel tartozik hozzá. Ha sok ilyen kísérletsorozatot végzünk el, akkor tapasztalataink (és modellünk) szerint egy adott esemény átlagosan annyiszor következik be, ahányféle lehetséges kimenetel tartozik hozzá. Ez vezet a Laplace-féle klasszikus modellhez:

Itt p a valószínűséget, A pedig egy adott eseményt jelent. Természetesen ügyelnünk kell arra, hogy az „összes esetek száma” olyan eseteket tartalmazzon, melyek bekövetkezése egyformán valószínű, ezek az úgynevezett elemi események. Annak eldöntésére, hogy mely események vehetők elemi eseményeknek, megint csak a modellhez kell nyúlnunk: ha sok kísérletet végezve lényegében egyforma számban következnek be ezek az elemi események, akkor mondhatjuk, hogy ezek valószínűsége megegyezik.
A biztos esemény valószínűsége 1, mivel itt minden eset jó eset, a lehetetlen esemény valószínűsége 0, mivel itt egyetlen jó eset sincs. (De vigyázat! Az, hogy egy esemény valószínűsége 1, nem feltétlenül jelenti azt, hogy a biztos eseményről van szó; ugyanígy az, hogy egy esemény valószínűsége 0, nem feltétlenül jelenti azt, hogy a lehetetlen eseményről van szó. A klasszikus valószínűségszámítási modellben igen, amikor véges sok kísérletet hajtunk végre, és az esetek száma véges sok. Azonban lehet végtelen kísérletsorozatokat is végrehajtani, illetve a geometriai modellben is lehet „végtelen sok eset” problémával találkozni; és itt már a fenti megállapításokat konkrét példákkal is illusztrálni lehet.)

Felmerült az a kérdés az előzőekben, hogy a klasszikus modell alkalmazásakor milyen eseményeket tekinthetünk elemi eseményeknek. Ez a kérdés már régen felmerült, és az úgynevezett „három kocka” problémájaként volt ismeretes. Ez a következőképpen hangzott:

Ha három kockával dobunk, akkor ugyanannyiféleképpen dobhatunk összesen 9-et, mint 10-et:

Ha azonban elkezdünk dobálni három kockával, akkor azt tapasztaljuk, hogy az összeg gyakrabban lesz 10, mint 9. Mi lehet ennek az oka? Amikor azt mondtuk, hogy ugyanannyiféleképpen dobhatunk a három kockával 10-et és 9-et, akkor az elemi eseményeknek tulajdonképpen azt tekintettük, hogy a dobott számokat nagyságrendi sorrendbe rakva hogyan kaphatjuk meg a 10-et illetve a 9-et, azaz elemi eseményeknek az 1, 2, ..., 6 számokból összeállítható rendezetlen hármasokat vettük. De van-e jogunk ehhez? Ha a sorbarendezést nem engedjük meg (tehát az elemi eseményeket a rendezett számhármasok jelentik), akkor a 10-et már nem ugyanannyiféleképpen kaphatjuk meg, mint a 9-et. A táblázatban szereplő számhármasokat többször kell számolni a sorbarendezéseknek megfelelően, így a 10 esetén 27 lehetőségünk van, míg a 9 esetén csak 25. Hogyan lehet igazságot tenni? Mivel azt szeretnénk, hogy a gyakorlatban lejátszódó véletlen eseményeket tudjuk modellezni, ezért végre kell hajtanunk a három kocka dobásának kísérletét sokszor, és meg kell nézni, hogy melyik modell írja le jobban a megfigyelt jelenséget. A tapasztalat azt mutatja, hogy az a modell áll közelebb a valósághoz, amelyben nem tekintünk el a kockák dobási sorrendjétől.

Erre persze mondhatja valaki, hogy a három teljesen egyforma kinézetű, azonos anyagból készült, minden szempontból egyforma kockát mi különbözteti meg egymástól? Honnan tudhatjuk, hogy melyik melyik?

Végezzük el a következő gondolatkísérletet: Vegyünk három teljesen egyforma dobókockát, és fessük be őket pirosra, zöldre, kékre. Adjuk őket oda egy normális embernek, és dobáltassuk fel a kockákat. Ő meg tudja különböztetni a kockákat egymástól, hisz azok különböző színűek. Sok kísérlet végrehajtása után kap valamiféle relatív gyakoriságot a lehetséges értékekre. Ezután adjuk oda a kockát egy színvaknak, aki számára a három kocka teljesen egyforma, hiszen nem látja a színüket. Ha ő dobál a kockákkal, akkor nyilvánvalóan ugyanazt az eredményt kell kapja az egyes értékek relatív gyakoriságára, hiszen a kockák nem tudják, hogy most éppen egy színvak dobál velük, tehát nyilvánvalóan ugyanúgy viselkednek, mint eddig. Vegyük le ezután a színezést a kockákról, és adjuk vissza a normális embernek. Az ő kezében a kockák ugyanúgy kell viselkedjenek, mint a színvak ember kezében, hiszen a kockák arról sem tudnak, hogy be vannak-e színezve. Ebből a gondolatmenetből viszont az következik, hogy a megkülönböztető jellel ellátott kockák ugyanúgy viselkednek, mint a nem megkülönböztethető kockák. Tehát a sorrendet figyelembe kell vennünk a dobott értékeknél.

Hasonlóan kiváló terep az elemi események előfordulásának vizsgálatára az úgynevezett kockapóker játék. Ebben 5 kockával dobunk, és a klasszikus pókerszabályoknak megfelelően értékeljük a kapott számötöst (azaz a kiértékelésnél nem számít a dobási sorrend). A lehetőségek:

egy pár:              2 egyforma + 1 + 1 + 1 szám (pl. 3, 4, 5, 1, 3)

két pár:               2 egyforma + 2 egyforma + 1 szám (pl. 3, 5, 4, 3, 5)

terc vagy drill:   3 egyforma + 1 + 1 szám (pl. 2, 3, 4, 2, 2)

sor:                      5 egymást követő szám, tetszőleges sorrendben (pl. 2, 3, 1, 4, 5)

full:                     3 egyforma + 2 egyforma szám (pl. 3, 2, 3, 3, 2)

póker:                 4 egyforma + 1 szám (pl. 3, 4, 3, 3, 3)

royal póker:       5 egyforma szám

Kérdés, hogy mekkora valószínűsége van az egyes lehetőségek bekövetkeztének? A kérdés megválaszolása szempontjából nem érdektelen, hogy a dobott számok sorrendjét is figyelembe vesszük az egyes lehetőségekhez tartozó „jó esetek” megszámolásánál, vagy pedig a dobási sorrendtől eltekintve határozzuk meg az esetek számát. A függelékben részletezett számítások szerint az egyes lehetőségekhez az alábbi „jó eset”-számok tartoznak, attól függően, hogy a sorrendet figyelembe vettük-e avagy sem:

Látható, hogy  a táblázat két oszlopa elég jelentősen eltérő adatokat tartalmaz. Hogy lehet eldönteni tehát, hogy a táblázat melyik oszlopát tekintsük érvényesnek a gyakorlati problémákban?

Egy osztálynyi tanuló (kb. 30 fő) mindegyike dobjon 50-szer az 5 db kockával, és jegyezze fel a kapott eredményeket a táblázatba. Utána összesítsék a tanulók a kapott eredményeket kimenetelenként, és ha ezen számok aránya az 1. oszlop arányainak megfelel, akkor a sorrendet figyelembe kell vennünk, ha a 2. oszlop arányainak felel meg, akkor a sorrendet nem kell figyelembe vennünk.

A tapasztalat azt mutatja már ilyen viszonylag kevés dobás esetén is, hogy a számok az 1. oszlop arányait mutatják, tehát a sorrendet figyelembe kell vennünk.

Jó-jó, mondhatja még mindig a kételkedő, de mi van azokkal a problémákkal, ahol nyilvánvalóan nem kell megkülönböztetnünk a sorrendet? Vegyük például a lottóhúzást! Ott már tényleg nem kell foglalkozni a sorrendi problémákkal! Valóban így van ez? Járjuk körbe ezt a kérdést alaposabban!

A következő kijelentéssel elég gyakran lehet találkozni:

A lottó ötös kihúzásának valószínűsége , (az összes esetek száma (eltekintve a húzási sorrendtől, hiszen az nem számít), és a jó

esetek száma 1, feltéve, hogy csak 1 szelvény töltöttünk ki).

Ha a klasszikus modellt a húzási sorrend figyelembevételével alkalmazzuk, akkor az összes esetek száma 90*89*88*87*86, a jó esetek száma pedig 1, hiszen továbbra is csak 1 lottót töltöttünk ki, tehát az eredmény nem ugyanaz, mint az előbb. Igen ám, csakhogy ha a sorrendet figyelembe vesszük a húzásnál, akkor figyelembe kell vennünk a lottószelvényünk kitöltésénél is! Az egy darab lottószelvényt 5*4*3*2*1 -féleképpen tölthetjük ki ugyanazokkal a számokkal, hiszen a beikszelést annyiféleképpen végezhetjük, ahányféleképpen az öt általunk kiválasztott számot sorbarakhatjuk. Tehát az összes esetek száma , amit átalakítva, és felhasználva a  egyenlőséget az

összefüggést kapjuk, tehát a kétféleképpen számolt valószínűség megegyezik.

Ha az átalakítást részletesebben megnézzük, akkor ki is derül ennek oka: amikor nem vesszük figyelembe a sorrendet, akkor tulajdonképpen az történik, hogy csoportosítjuk az elemi eseményeket: azokat a húzásokat, amelyekben ugyanazok a számok szerepelnek, egy kupacba tesszük, és „újfajta” elemi eseménynek tekintjük. Minden „újfajta” elemi esemény ugyanannyi régi elemi eseményből tevődik össze, ezért a sorrend figyelembe vételekor kapott hányadosban a számlálót és a nevezőt ugyanazzal a számmal kell leosztanunk, hogy a sorrend nélküli eset hányadosát kapjuk, így az eredmény nyilvánvalóan ugyanaz lesz.

Ez egyben azt is mutatja, hogy a sorrendet figyelembe véve mindig helyes eredményt kaphatunk, de számolásunkat leegyszerűsítheti a sorrendtől való eltekintés. Mikor lehet ezt megtenni? Erre is választ kaptunk: akkor, ha az elemi események beoszthatóak egyforma elemszámú csoportokba olyan módon, hogy minden csoportban olyan elemi események kerüljenek, melyek egymástól csak sorrendben térnek el, és az összes ilyen esemény bekerült az adott csoportba. Az is látszik, hogy ez a csoportba osztás nem tehető meg pl. a visszatevéses húzásnál a húzási sorrend alapján megkülönböztetett események esetén, hiszen ekkor a különböző elemeket tartalmazó húzásokat a sorrend szerint nem ugyanannyiszor számoljuk meg, mint az egyforma elemeket is tartalmazó húzásokat.

A legtöbb véletlen esemény modellezésére alkalmas az úgynevezett urna-modell. Legyen egy adott esemény bekövetkezésének valószínűsége . Tegyünk egy urnába K db fehér, és N – K db

fekete golyót, és húzzunk ki egy golyót az urnából. Ekkor az esemény bekövetkezte megfelel a fehér golyó húzásnak, az esemény be nem következte a fekete golyó húzásnak.

Ennek segítségével ki tudjuk számítani, hogy pl. n db kísérletből hányszor következik be egy adott esemény. Az előzőekben ismertetett urnából húzzunk n-szer, visszatevéssel (tehát a kihúzott golyót mindig visszatesszük, azaz mindig eséllyel húzunk fehéret).

Mi a valószínűsége, hogy k-szor húztunk fehér golyót? (Azaz mi a valószínűsége, hogy az A esemény k-szor következett be?)

Használjuk a klasszikus modellt. Az összes húzások száma N az n-ediken, a jó esetek száma, amikor k db fehéret és n-k db feketét szerepeltetünk: (*), így a keresett valószínűség

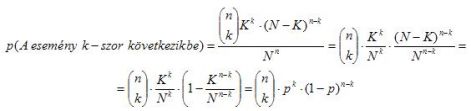
(*) Megjegyzés: Először ki kell jelölnünk a k db fehér golyó helyét, ezt -féleképpen tehetjük meg, majd kiválasztjuk a k fehéret


visszatevéssel a K golyó közül, amelyeket a korábbiakban mondottak miatt megkülönbözethetőnek veszünk, -féleképpen, és az n – k feketét az N – K fekete közül -féleképpen.

II.3. Műveletek eseményekkel; kapcsolat a valószínűségek között

Az eseményekkel való műveletek között két legfontosabbat különböztetünk meg:

a) események szorzata: Az A esemény és B esemény szorzatán azon eseményt értjük, melyben A és B esemény együttesen bekövetkezik. Jelölése: AB. [Úgy is megfogalmazhatnánk, hogy az AB esemény minden esetben bekövetkezik, amikor A és B együttesen bekövetkezik.